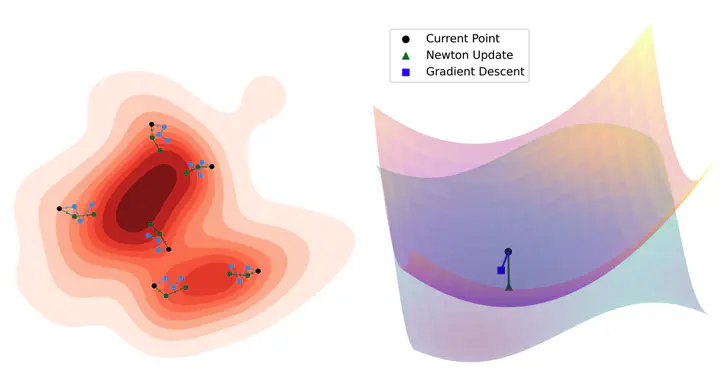
Conceptual overview of the SVN method. The green curvature-informed SVN updates are much higher quality and require fewer steps than the corresponding blue SVGD ones.Abstract
Deep neural network ensembles are powerful tools for uncertainty quantification, which have recently been re-interpreted from a Bayesian perspective. However, current methods inadequately leverage second-order information of the loss landscape, despite the recent availability of efficient Hessian approximations. We propose a novel approximate Bayesian inference method that modifies deep ensembles to incorporate Stein Variational Newton updates. Our approach uniquely integrates scalable modern Hessian approximations, achieving faster convergence and more accurate posterior distribution approximations. We validate the effectiveness of our method on diverse regression and classification tasks, demonstrating superior performance with a significantly reduced number of training epochs compared to existing ensemble-based methods, while enhancing uncertainty quantification and robustness against overfitting.
This paper introduces the Stein Variational Newton Ensemble method, a novel approach to Bayesian inference in deep learning. By integrating scalable second-order information through Hessian approximations, this method enhances the training efficiency and uncertainty quantification of neural network ensembles. Experiments demonstrate its superiority over existing methods in regression and classification tasks, offering a promising direction for robust and efficient deep learning.
View the paper on arXiv or explore the GitHub repository for implementation details.